[AI810 Blog Post (20255036)] Generative Models for Inorganic Crystals & Metal-Orgranic Frameworks

In this blog post, we review two recent works on generative models for crystals. One is SymmCD, which generates inorganic crystals by leveraging their special symmetry properties. The other is MOFDiff, which generates metal-organic frameworks by (MOFs) by exploiting their modular nature.

$$ \newcommand{\cM}{\mathcal{M}} \newcommand{\cA}{\mathcal{A}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bbR}{\mathbb{R}} $$

Motivation

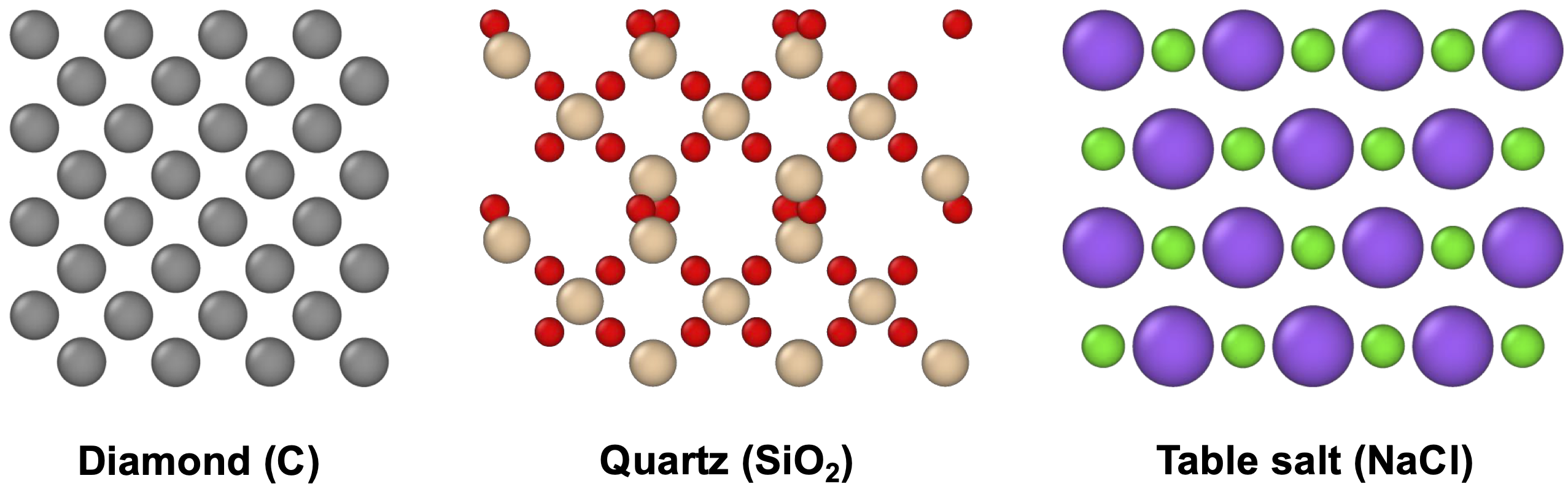
Materials span a wide range of structural and chemical complexities, from amorphous polymers to highly ordered solids. Among them, crystals refer to materials with a regular, repeating arrangement of atoms or molecules. Many everyday materials are crystalline (Figure 1): diamond, known for its extreme hardness; quartz, used in electronics; and table salt, essential in daily life. Designing new crystalline materials with desirable properties is at the heart of breakthroughs in energy, electronics, and environmental sustainability.

In recent years, generative models have gained attention as powerful tools for automating the design of novel crystal structures. Most existing work focuses on inorganic crystals, which include materials like semiconductors, superconductors, and catalysts. More recently, some attention has turned to metal-organic frameworks (MOFs), a crystalline materials composed of metal clusters and organic linkers. Their porous structures and high tunability make them promising candidates for gas storage, catalysis, and drug delivery.

Two Types of Crystals, Two Types of Challenges

Figure 2. Examples of inorganic crystals and metal-organic frameworks.

While both inorganic crystals and MOFs are crystalline materials, their fundamental differences introduce distinct challenges for generative modeling (Figure 2):

Inorganic crystals typically contain fewer atoms per structure and exhibit high degrees of symmetry. However, they lack natural subunits, making them difficult to decompose or simplify for modeling.
MOFs, in contrast, often consist of hundreds to thousands of atoms per structure. Fortunately, their modular nature allows them to be decomposed into well-defined building blocks: metal nodes and organic linkers.

	Inorganic	MOF
Size	~10-50 atoms/structure	~50-2000 atoms/structure
Key structural trait	Symmetry-rich	Modular
Generation challenge	Capturing symmetry	Scaling to large structures

In this blogpost, we explore two recent generative models that address these distinct challenges:

SymmCD (ICLR 2025) targets inorganic crystals using a diffusion model that explicitly incorporates symmetry. By learning to generate only the asymmetric unit and expanding it via symmetry operations, it ensures validity and efficiency in generation.
MOFDiff (ICLR 2024) focuses on MOFs by leveraging their modularity through a coarse-grained representation. By learning to generate the coarse-grained representation, MOFDiff succesffully generates large and complex MOF structures.

The following table provides a quick summary of the two works:

	SymmCD	MOFDiff
Target material	Inorganic crystals	Metal-organic frameworks
Dataset	Materials Project	BW-DB
Key idea	Generate asymmetric unit and reconstruct full structure using symmetry	Generate coarse-grained MOF structure based the modular nature of MOFs
Method	Diffusion	Diffusion
Publication	ICLR 2025	ICLR 2024

SymmCD: Symmetry-Preserving Crystal Generation with Diffusion Models

Preliminary: Representing Crystals

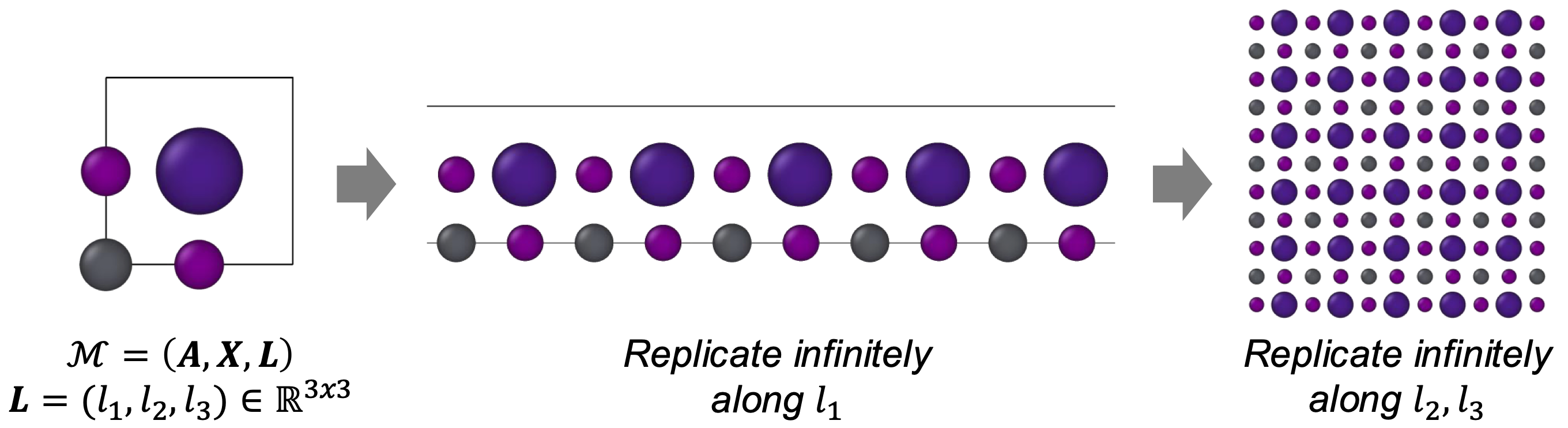
Figure 3. The unit cell representation of a crystal. The ideal, infinite crystal structure can be recovered by replicating the cell along the three lattice vectors.

To represent a 3D structure of a molecule with $N$ atoms, we typically specify two components:

The atom types $\bA=(a_1, \dots, a_N) \in \cA^N$, where each $\cA$ is the set of possible elements,
The 3D coordinates of those atoms, $\bX=(x_1, \dots, x_N) \in \bbR^{N \times 3}$.

Crystals are similar, but with one key addition: the lattice. The lattice is defined by three lattice vectors $\mathbf{L}=(l_1, l_2, l_3) \in \bbR^{N \times 3}$ which describe how the unit cell repeasts in space. This compact unit cell representation $\cM = (\bA, \bX, \bL)$ contains all the information needed to define a crystal. By translating the atoms along the lattice vectors $l_1, l_2, l_3$, we can reconstruct the full (theorectically infinite) periodic structure of the crystal (Figure 3).

Asymmetric Unit and Site Symmetries

Figure 4. (left) An asymmetric unit can be unfolded using symmetry operations to reconstruct the full unit cell. (right) SymmCD generates the asymmetric unit, which contains the atom types, coordinates, lattice, and site symmetries.

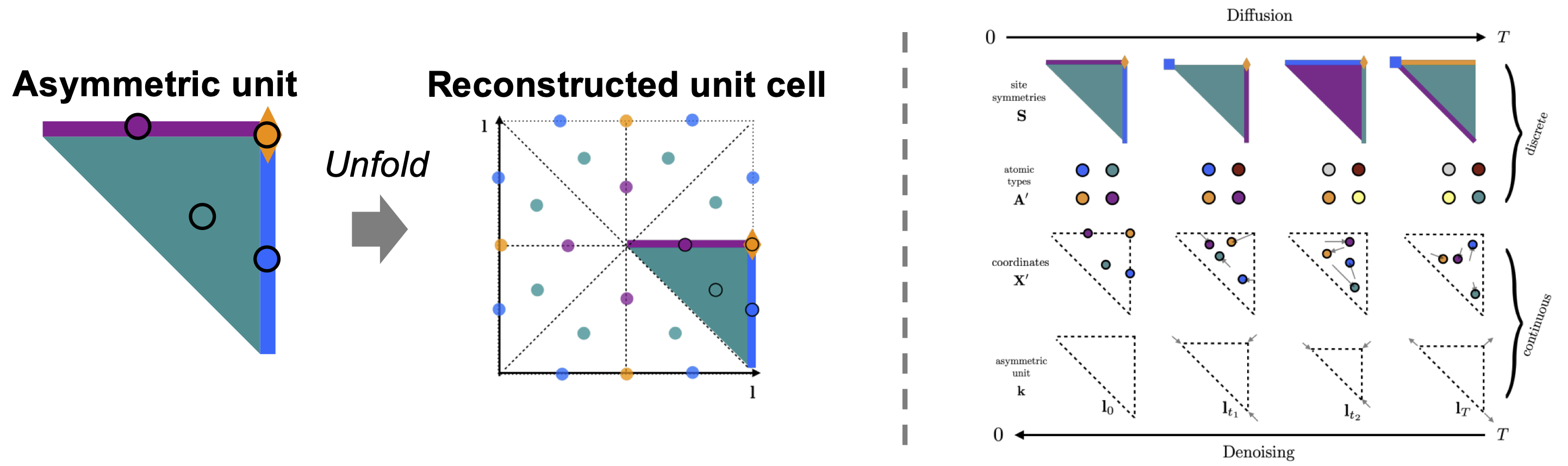
While the unit cell representation $\cM = (\bA, \bX, \bL)$ compactly represents a crystal, SymmCD uses an even smaller representation: the asymmetric unit. The asymmetric unit can be combined with crystal symmetry operations to reconstruct the full unit cell (Figure 4, left).

A useful analogy for understanding the asymmetric unit is cutting a paper snowflake: the folded paper represents the asymmetrc unit, and unfolding aplies the symmetry to create the full pattern of the paper snowflake.

But here’s the subtle part: where you make the cut affects how many times it appears in the final pattern. For instance, a cut at the center of the folded paper is repeated six times, while a cut at an edge appears three times. In crystallography, this concept is captured by the site symmetry – it tells you how to replicate an atom based on its position on the asymmetric unit.

SymmCD leverages these two simple concepts for inorganic crystal generation. Rather than generating the full crystal, it generates just the asymmetric unit, which contains the atom types, coordinates, lattice, and site symmetries (Figure 4, right). This simplifies the generation process while guaranteeing that the resulting structures are symmetric.

Mathematically, we represent an asymmetric unit with:

Atom types $\bA' = (a_1', \dots, a_M') \in \cA^M$,
3D coordinates $\bX=(x_1', \dots, x_M') \in \bbR^{M \times 3}$,
Asymmetric lattice $\mathbf{k} \in \mathbb{R}^6$ (see the paper for details), and
Site symmetries $\bS = (S_{x_1'}, \dots, S_{x_M'}) \in \mathcal{P}^M$, where $\mathcal{P}$ denotes the set of all possible site symmetries.

Note that $M \leq N$, since the asymmetric unit contains only a subset of the atoms in the full unit cell.

SymmCD: Pre-processing, Training, and Sampling

Figure 5. The full pipeline of SymmCD, including pre-processing, training, sampling, and post-processing.

Pre-processing: Extracting the Asymmetric Unit

Recall that the core idea of SymmCD is to model the asymmetric unit rather than the entire unit cell. But how do we extract the asymmetric unit from a given crystal?

Crucially, all crystals belong to one of just 230 space groups, each defining a unique set of symmetry operations. Given a crystal in unit cell form, $\cM = (\bA, \bX, \bL)$, we first determine its space group $G$ – this can be done using tools such as spglib. The space group encodes the symmetries present in the crystal, which in turn define its asymmetric unit.

Using this information, we convert the dataset from unit cell representation to asymmetric unit cell representation as follows: $\begin{equation} \mathcal{D} = \{ (\bA, \bX, \bL) \} \Rightarrow{} \mathcal{D} = \{ (G, \mathbf{k}, \bA', \bX', \bS) \}. \end{equation}$

Training the Model

SymmCD models the joint distribution over asymmetric unit components and the space group as: $\begin{equation} p_{\theta}(G, \mathbf{k}, \bA', \bX', \bS)=p_{\theta}(\mathbf{k}, \bA', \bX', \bS \vert G)p(G). \end{equation}$

That is, once a space group $G$ is specified (or sampled), the model generates a compatible asymmetric unit $(\mathbf{k}, \bA', \bX', \bS)$. To achieve this, SymmCD trains an E(3)-equivariant graph neural network (GNN), where the atom types and site symmetries $\bA', \bS$ are learned with discrete diffusion and the lattice $\mathbf{k}, \bX'$ are learned with continuous diffusion.

Sampling and Post-processing

Generating inorganic crystal structures with SymmCD involves three main steps:

Select a space group $G$ – either randomly or based on desired properties.
Sample asymmetric unit $(\mathbf{k}, \bA', \bX', \bS)$ using the trained diffusion model.
Project the generated atoms into valid Wyckoff positions based on their site symmetries.

Why is this projection step necessary? Recall the paper snowflake analogy: a cut made at the center is repeated more times than one near the edge. In crystals, certain regions of the asymmetric unit permit only specific site symmetries. If a generated atom-site symmetry pair is invalid, its position must be projected a location compatible with the symmetry constraints.

Finally, the full unit cell $\cM = (\bA, \bX, \bL)$ is reconstructed by applying the symmetry operations associated with each atom’s site symmetry. By generating only the asymmetric unit, SymmCD reduces computational complexity while ensuring symmetric outputs.

Experimental Results: SymmCD Generates Diverse and Novel Crystals

Figure 6. Comparison of crystals generated by SymmCD and baseline models. (left) Distribution of space group symmetries across generated samples. (middle) Number of novel (unseen) structures produced by each model. (right) Example crystal generated by SymmCD with space group Pmmm.

In the experiments, 10,000 crystals are generated from each model and evaluated based on the distribution of space group symmetries and novelty.

Both SymmCD and DiffCSP++ generate crystals spanning a wide range of space group symmetries, demonstrating their capacity to model diverse crystal types (Figure 6, left). However, SymmCD achieves higher novelty, since it learns to generate asymmetric units from scratch, whereas DiffCSP++ relies on refining known templates (Figure 6, middle). Figure 6, right shows an example crystal generated by SymmCD with space group Pmmm, demonstrating the model’s ability produce valid and symmetric structures.

MOFDiff: Coarse-grained Diffusion for Metal-Organic Framework Design

Preliminary: Coarse-grained Representation for MOFs

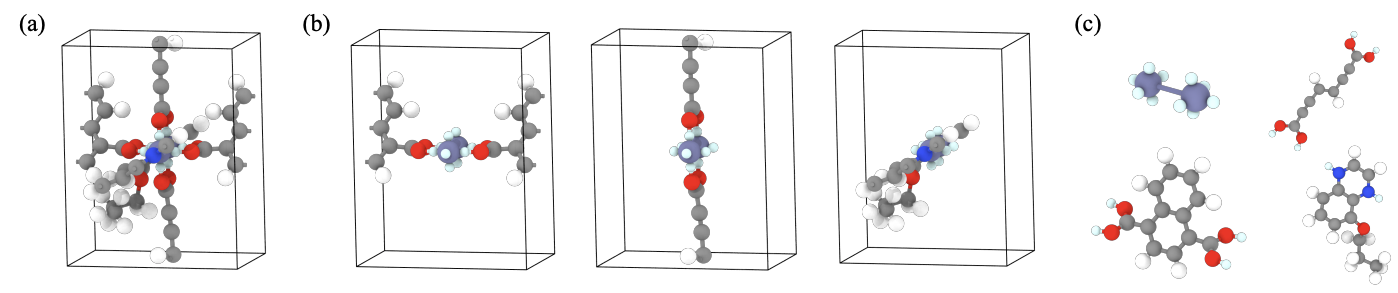
Figure 7. Decomposing a MOF into its building blocks. (a) An example MOF unit cell. (b) Metal node and organic linkers visualized one at a time for visual clarity. (c) All four building blocks in the example. The blue dumbbell-shaped building block is metal, while others are organic.

Metal–Organic Frameworks (MOFs) are one of the structurally complex materials known. Compared to inorganic crystals, they are much larger, often containing hundreds to thousands of atoms per unit cell. This scale makes atom-level generative modeling both inefficient and prone to poor performance.

Fortunately, MOFs come with a built-in advantage: modularity. Each MOF is composed of building blocks called metal clusters and organic linkers (Figure 7). Therefore, instead of representing MOFs as full atomic structures $(\bA, \bX, \bL)$, MOFDiff uses a simplified, coarse-grained representation $\begin{equation} \cM^C = (\bA^C, \bX^C, \bL) \end{equation}$ where:

$\bA^C = (a_1^C, \dots, a_K^C) \in \mathbb{B}^{K}$ are the building block types (e.g., a metal node or linker),
$\bX^C = (x_1^C, \dots x_K^C) \in \bbR^{K \times 3}$ are their 3D Cartesian coordinates, and
$\bL$ is the lattice that defines periodicity (same as unit cell representation).

The core idea behind MOFDiff is to learn this coarse-grained representation instead of modeling the full atomic structure. Since $K \ll N$, this representation is much more efficient to model.

Learning Building Block Representations

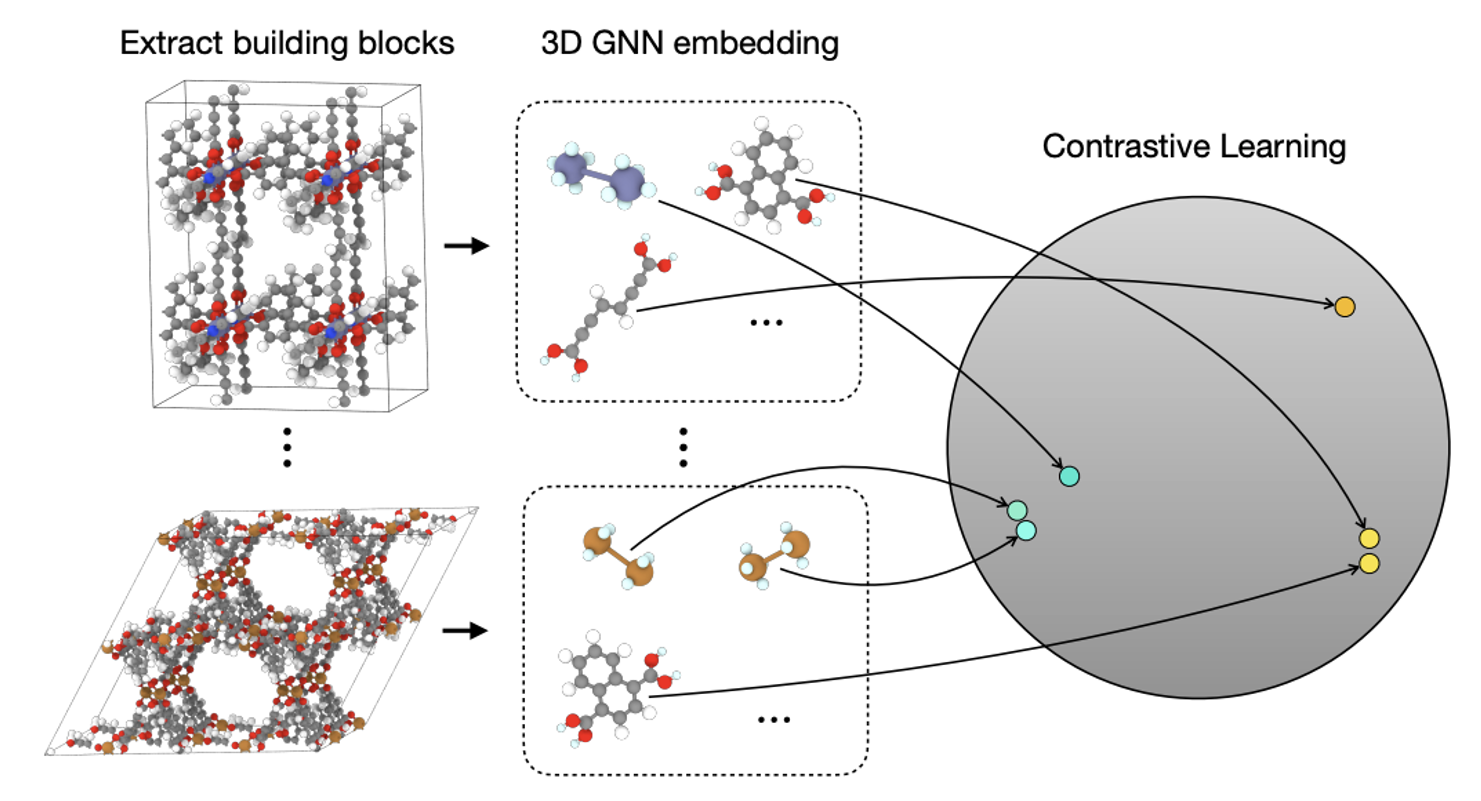
How do we represent these building blocks effectively?

A naive approach might be to extract all building blocks from the training dataset, assign each a one-hot encoding, then train a diffusion model: discrete diffusion for the building block types $\bA^C$, and continuous diffusions for their positions $\bX^C$ and lattice $\bL$.

However, the training dataset contains around 2 million of building blocks, which makes one-hot encoding extremely sparse and hard to learn. Also, many of these building blocks are topologically identical – they have the same atom and bond structure (i.e., same 2D graph), differing only slightly in 3D geometry, making this representation very inefficient.

To overcome this, MOFDiff learns a dense, continuous embedding $\bA^C$ for each building block that captures topological similarity. It does this by training a SE(3)-invariant graph neural network takes as input the $i$ building block (i.e., its atom types and coordinates) and outputs a dense embedding $\mathbf{b}_i \in \bbR^d$ corresponding to that building block.

To ensure that the learned embeddings group similar building blocks together, MOFDiff uses a contrastive learning objective (Figure 8). Specifically, it first computes ECFP4, a molecular fingerprint which encodes topological information, then trains the models with a contrastive loss that brings structures with same ECFP4 close together in the embedding space.

The contrastive loss is defined as: $\begin{equation} \mathcal{L}_C = - \log \sum_{i \in \mathbf{B}} \left( \frac{\sum_{j \in \mathbf{B}_i^{+}} \exp(s_{i,j} / \tau)}{\sum_{j \in \mathbf{B} \setminus \{i\}} \exp(s_{i,j} / \tau)} \right) \end{equation}$ where

$\mathbf{B}$ is a batch of building blocks,
$\mathbf{B}_i^{+} \subseteq \mathbf{B}$ are building blocks with the same ECFP4 fingerprint as $i$,
$s_{i,j}$ is the cosine similarity between projected building block embeddings:
$\begin{equation} s_{i,j} = \frac{\mathbf{p}_i^{\top} \mathbf{p}_j}{\|\mathbf{p}_i\| \|\mathbf{p}_j\|}, \quad \mathbf{p}_i = \operatorname{MLP}(\mathbf{b}_i) \end{equation}$
$\tau$ is the temperature.

Once trained, this encoder maps each building block to a dense vector embedding. All MOFs in the dataset can then be transformed into their coarse-grained representation $\cM = (\bA^C, \bX^C, \bL)$, where $\bA^C = (\mathbf{b}_1, \dots, \mathbf{b}_K) \in \bbR^{K \times d}$ is the dense embedding. The paper uses $d=32$, which is much more compact representation than a one-hot encoding over ~2M types of building blocks.

Training MOFDiff

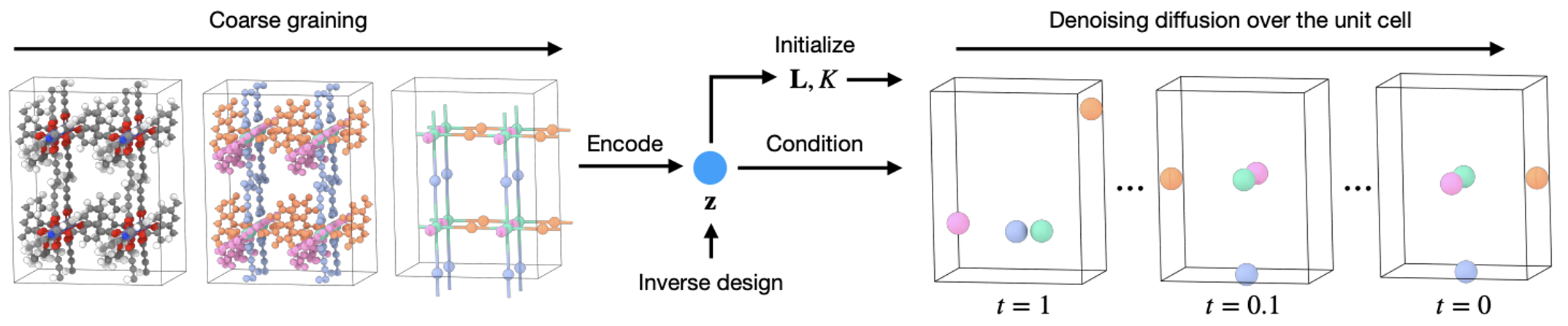
With the coarse-grained representation in place, it’s time to train the generative model (Figure 9).

MOFDiff aims to model the full joint distribution over the coarse-grained structure and an additional latent variable $\mathbf{z}$: $\begin{equation} p_{\theta}(\bA^C, \bX^C, \bL, K, \mathbf{z}) = p_{\theta}(\bL, K \vert \mathbf{z}) p_{\theta}(\bA^C, \bX^C \vert \bL, K, \mathbf{z}), \end{equation}$ where:

$\bA^C=(\mathbf{b}_1, \dots, \mathbf{b}_K) \in \bbR^{K \times d}$ and $\bX^C = (x_1^C, \dots x_K^C) \in \bbR^{K \times 3}$ are the building block types and positions,
$\bL$ is the lattice,
$\mathbf{z}$ is a latent vector used for generating the $\bL$, $K$.

MOFDiff factorizes this distribution as: $\begin{equation} p_{\theta}(\bA^C, \bX^C, \bL, K, \mathbf{z}) = p_{\theta}(\bL, K \vert \mathbf{z}) p_{\theta}(\bA^C, \bX^C \vert \bL, K, \mathbf{z}). \end{equation}$

The first part, $p_{\theta}(\bL, K \vert \mathbf{z})$ is modeled using an MLP: $\begin{equation} \hat{\bL}, \hat{K} = \operatorname{MLP}_{\bL, K}(\mathbf{z}), \end{equation}$ while the second part, $p_{\theta}(\bA^C, \bX^C \vert \bL, K, \mathbf{z})$ is modeled using score-based diffusion, where a periodic graph neural network denoiser $\operatorname{PGNN}_D$ predicts the noise in the atom types and coordinates as: $\begin{equation} \mathbf{s}_{\bA^C}, \mathbf{s}_{\bX^C} = \operatorname{PGNN}_D(\tilde{\cM}_t^C, \mathbf{z}). \end{equation}$ Here, $\tilde{\cM}_t^C=(\bA_t^C, \bX_t^C, \bL)$ is the noised version of the coarse-grained structure at timestep $t$ and $\mathbf{z}$ is the latent vector produced with a periodic graph neural network encoder $\operatorname{PGNN}_E$: $$ \begin{equation} \mathbf{z} = \operatorname{PGNN}_E(\cM^C). \end{equation}

Objective function

The denoiser $\operatorname{PGNN}_D(\cM_t^C, z)$ is trained using the standard denoising score objective: $\begin{equation} \mathcal{L}_{\boldsymbol{A}}=\mathbb{E}_{t, \boldsymbol{M}^C, \boldsymbol{\epsilon}_{\boldsymbol{A}}}\left[\left\|\boldsymbol{\epsilon}_{\boldsymbol{A}}-\boldsymbol{s}_{\boldsymbol{A}_t^C, \mathbf{z}}\right\|^2\right], \quad \mathcal{L}_{\boldsymbol{X}}=\mathbb{E}_{t, \boldsymbol{M}^C, \boldsymbol{\epsilon}_{\boldsymbol{X}}}\left[\sigma_t^2\left\|\boldsymbol{\epsilon}_{\boldsymbol{X}}-\boldsymbol{s}_{\boldsymbol{X}_t^C, \mathbf{z}}\right\|^2\right]. \end{equation}$ $\operatorname{MLP}_{\bL, K}(\mathbf{z})$ is supervised with the mean squared error and cross-entropy loss: $\begin{equation} \mathcal{L}_{\boldsymbol{L}, K}=\|\boldsymbol{L}-\hat{\boldsymbol{L}}\|^2+\operatorname{CrossEntropy}(K, \hat{K}). \end{equation}$ Finally, the encoder $\operatorname{PGNN}_E$ is regularized with a KL divergence $\mathcal{L}_{\mathrm{KL}}$ to match a standard normal prior.

The overall training objective for MOFDiff combines all components as: $\begin{equation} \mathcal{L}_{\text {MOFDiff }}=\mathcal{L}_{\boldsymbol{A}}+\mathcal{L}_{\boldsymbol{X}}+\mathcal{L}_{\boldsymbol{L}, K}+\beta_{\mathrm{KL}} \mathcal{L}_{\mathrm{KL}}. \end{equation}$ where $\beta_{\mathrm{KL}}$ is a hyperparameter that controls the strength of KL regularization, set to 0.01.

Sampling Pipeline for MOFDiff

Figure 10. Post-processing pipeline for MOFDiff. Once we sample a coarse-grained structure, we should (1) decode the building block identities, (2) rotate the building blocks with a self-assembly process, and (2) relax structure with UFF force field.

Figure 11. The illustration of self-assembly process. The self-assembly processes maximizes the connection between building blocks (connection points are shown in light blue).

Once MOFDiff is trained, we can generate a new MOF structure with the following process:

Sample a random latent code $\mathbf{z} \sim \mathcal{N}(0,I)$.
Predict the lattice and number of building blocks: $\begin{equation} \hat{\bL}, \hat{K} = \operatorname{MLP}_{\bL, K}(\mathbf{z}) \end{equation}$
Run denoising diffusion with the trained denoiser $\operatorname{PGNN}_D(\tilde{\cM}_t^C, \mathbf{z})$ to generate the coarse-grained structure $(\bA^C, \bX^C, \bL)$.

At this point, we have a coarse-grained MOF. We now need to recover the full atomic structure with fine-grained details. Here’s how (Figure 10):

Building block decoding. For each generated embedding $\bA^C$, we find the building block from the training dataset that has the closest embedding with nearest neighbor search. We then retrieve actual atom types and coordinates of this closest building block.
Self-assembly process. Since we have only predicted the center of mass of each building block with $\bX^C$, we now need to know how to rotate them. MOFDiff uses an optimization-based sef-assembly algorithm to find the rotation that maximizes the alignment of connection points between the building blocks (Figure 11).
Force field relaxation. Finally, the assembled structure undergoes relaxation with energy minimization with the UFF force field. This step ensures that we can make a fine-grained refinement to get the final structure.

Evaluation Results: MOFDiff generates high-quality MOFs

Figure 12. Results for MOFDiff. (left) Validity, novelty, and uniqueness (VNU) of generated structures. (middle) CO2 working capacity distribution of MOFDiff and the training dataset. (right) Promising MOFs with high CO2 capacity sampled with MOFDiff.

Generating Valid, Novel, and Unique MOFs

How does MOFDiff perform in practice? To evaluate it, the authors sampled 10,000 MOF structures and assessed them on three key metrics: validity, novelty, and uniqueness.

Validity: A structure is considered valid if it passes the validity check with MOFChecker, which assesses whether a MOF is chemically and physically valid based on a set of criteria including the presence of at least one metal, carbon, and hydrogen atom; overlapping atoms; and valency.
Novelty: A structure is novel if it does not exist in the training dataset. This is measured with MOFid, which computes a unique identifier for a MOF based on its building blocks and connectivity.
Uniqueness: We find the unique structures by filtering out the duplicates from the generated set of structures.

Out of 10,000 generated structures, 3,012 passed the validity check and 2,998 were valid, novely, and unique (Figure 12, left). That’s nearly 3,000 high-quality MOFs generated from scratch – an impressive result given the structural complexity and the size of MOFs.

Discovering High-performing MOFs for Carbon Capture

Thanks to the latent variable $\mathbf{z}$, MOFDiff can also be used for property-guided generation.

Suppose you want to discover MOFs with high CO2 working capacity – a key metric for carbon capture technology. MOFDiff enables this by learning a simple property predictor $\begin{equation} \hat{\mathbf{c}} = \operatorname{MLP}_P(\mathbf{z}), \end{equation}$ where $\mathbf{c}$ is the property of interest (e.g., CO2 capacity). This predictor is trained with the mean squared error loss using known property labels.

To sample MOFs with desired properties, we can let MOFDiff generate many latent vectors $\mathbf{z} \sim \mathcal{N}(0, I)$, compute the CO2 working capacity $\hat{\mathbf{c}}$ with the trained predictor, and only decode $\mathbf{z}$’s with high CO2 working capacity.

In experiments, this approach successfully generates MOFs with higher CO2 working capcity than those in the training dataset, demonstrating MOFDiff’s potential for targeted material discovery (Figure 12, middle). We also show some examples of promising candidates generated by MOFDiff in Figure 12, right.